Abstract
In-home automated scoring systems are in high demand; however, the current systems are not widely adopted in clinical settings. Problems with electrode contact and restriction on measurable signals often result in unstable and inaccurate scoring for clinical use. To address these issues, we propose a method based on ensemble of small sleep stage scoring models with different input signal sets. By excluding models that employ problematic signals from the voting process, our method can mitigate the effects of electrode contact failure. Comparative experiments demonstrated that our method could reduce the impact of contact problems and improve scoring accuracy for epochs with problematic signals by 8.3 points, while also decreasing the deterioration in scoring accuracy from 7.9 to 0.3 points compared to typical methods. Additionally, we confirmed that assigning different input sets to small models did not diminish the advantages of the ensemble but instead increased its efficacy. The proposed model can improve overall scoring accuracy and minimize the effect of problematic signals simultaneously, making in-home sleep stage scoring systems more suitable for clinical practice.
Similar content being viewed by others
Introduction
Sleep is an essential element of one’s health. For example, lack of sleep and sleep disorders are known to cause serious diseases, such as diabetes, depression, stroke, and other cardiovascular diseases1,2,3,4. Considering that many people have sleep problems5, scaling up sleep diagnosis is necessary but challenging.
One reason for this challenge is that most sleep diagnostic inspections require hospitalization. This limits the number of inspections and diagnosable patients, making it difficult to scale up sleep diagnosis. Additionally, the workload for these inspections is significant6. For example, sleep stage scoring, which involves identifying sleep states from biological signals, is essential for sleep diagnosis and requires about two hours of labor from trained doctors or physicians.
To address these problems, several researchers and companies have developed in-home devices for sleep inspection, such as devices for biological signal measurements7,8,9,10,11,12,13. These in-home devices, combined with an automated diagnosis system14,15,16,17,18,19, have already been commercialized20,25,26. This paper primarily focuses on in-home signal measurement devices for automated sleep stage scoring.
However, this approach is not widely accepted for clinical purposes owing to two key issues related to scoring accuracy.
- Electrode contact problems:
-
In clinical inspections, sleep experts, such as doctors and physicians place measuring electrodes. Therefore, contact problems, such as disconnecting and electrode popping, are rare, and the measured signals are typically clear. In contrast, in-home measurement requires patients themselves to place the electrodes. Consequently, contact failures, as shown in Fig 1, occur more frequently, making it challenging to detect informative waveforms for identifying sleep stages. Additionally, noise caused by contact problems reduce scoring accuracy. For example, waveforms (artifacts) resulting from the electrode popping can resemble the K-complex waves, which are crucial for identifying Stage N2. Many existing automated scoring systems employ anti-noise methods to address these contact problems16. However, our experimental results indicate that these methods do not always perform as expected.
- Restriction of measurable signals:
-
In sleep clinics, sleep experts measure biological signals using polysomnography (PSG) equipment, which provides three types of biological signals: six electroencephalogram signals (EEG), two electrooculogram signals (EOG), and one submental electromyogram signal (EMG). In contrast to PSG equipment, in-home devices may provide restricted signals due to the limited number of measuring electrodes. This limitation makes it difficult to detect specific waveforms and accurately score sleep stages.
Examples of EEG signal montage by human experts. This example measures potentials at four locations: \(\textrm{Fp1}\), \(\textrm{Fp2}\), \(\textrm{M1}\), and \(\textrm{M2}\). The exemplified one-epoch potential signals from each electrode are included in the In-home EEG dataset used in the experiment. (a) Properly attached electrodes with standard potential differences between \(\mathrm{Fp1-M_{ave}}\), \(\mathrm{Fp2-M_{ave}}\), and \(\mathrm{Fp1-Fp2}\) used as EEG signals. (b) Application of the standard montage despite detachment of the \(\textrm{Fp2}\) electrode. This includes high-frequency noise overall, and K-complex-like waveforms can be seen in the \(\mathrm{Fp2-M_{ave}}\) signal, as highlighted within the area enclosed by the red dashed rectangle. (c)Modified montage due to detachment of the \(\textrm{Fp2}\) electrode. No noise is observed in these differential signals.
Based on this background, this research aims to develop a method to enhance scoring accuracy and mitigate its deterioration caused by contact problems. As a solution, we focus on a small-model ensemble approach, known for its simplicity and effectiveness in improving accuracy for classification tasks27,28. This method involves multiple classification models optimized with different training samples, employing majority voting to determine its output. This approach helps prevent overfitting and enhance classification accuracy.
The typical ensemble method is expected to contribute to improving scoring accuracy with limited numbers/types of signals; however, it does not address contact problems. Therefore, we decided to incorporate an additional step into our method.
Concept of the proposed method: the proposed method is an ensemble of six small models, each processing different input signals. (a) When all electrodes are measuring properly, the overall scoring result is based on the voting results of each small model. Here, ’voting’ refers to selecting the sleep stage with the highest total confidence score output by the small models. (b) In cases where there is a contact problem with an electrode (Fp2 in this example), voting is conducted using only the models that do not utilize the Fp2 electrode.
Fig 2 illustrates our concept using a four-electrode measurement device. Our proposed method is characterized by small models and a voting process. Unlike typical ensemble methods, it employs multiple models with different sets of input signals and electrodes (Table 1). In case where there is a problematic electrode, the small models associated with that electrode are excluded from the voting process.
This process mimics how experts address contact problems in manual scoring processes. Experts typically ignore noisy signals or perform “re-montage.” The biological signals are usually obtained by subtracting the electrical potentials of two electrodes, and re-montage involves changing this electrode pair. Therefore, our approach essentially mirrors these expert methods.
The concept of ignoring a problematic signal aligns with traditional anti-noise techniques. For example, certain automated sleep stage scoring methods estimate the contact states of electrodes and obtain clear signals from the two best electrodes16. However, this method limits the number of input signals regardless of the number of suitable electrodes. Therefore, the scoring accuracy tends to be suboptimal, particularly when all electrodes are properly attached.
In contrast, our method can use all healthy signals available in the scoring process. Therefore, the scoring accuracy may be less affected by the signal-ignoring process compared to the conventional anti-noise method. Additionally, if the accuracy of each small model is comparable, the proposed ensemble may also enhance scoring accuracy for clear records, akin to the typical ensemble methods27. In summary, our method may simultaneously achieve two objectives simultaneously, which the typical ensemble and traditional anti-noise methods attain. This study confirmed that this hypothesis holds for actual sleep records.
To evaluate the efficacy of the proposed method, we assessed the improvement in accuracy under conditions both with and without contact failures or losses. Experimental results from 297 whole-night sleep records obtained by our In-home EEG device demonstrated that the proposed ensemble method could enhance scoring accuracy in both scenarios, which the typical ensemble and anti-noise methods failed to achieve.
Sleep stage and its scoring process
Human sleep consists of five sleep stages: Wake, Rapid Eye Movement (REM), and Non-REM stages 1, 2, and 3 (N1, N2, and N3). Their percentages and transition between these stages can provide clues and evidence of sleep disorders, such as insomnia. The abstracted process for manual scoring29 involves several key steps:
- PSG signal acquisition:
-
Experts measure six EEG signals, two EOG signals, and one submental EMG signal from the patient.
- Preprocessing:
-
The signals are divided into 30-s sub-sequences called epochs. Each epoch serves as a unit of time for scoring, and one sleep-stage label is assigned to each epoch.
- Characteristic-wave detection:
-
Experts identify characteristic waves, waveforms unique to each sleep stage, from the PSG signals.
- Sleep stage assignment:
-
Experts assign one sleep stage following the AASM rule29, which primarily adheres to the following three principles:
-
If an epoch, especially its first half, contains the characteristic waves, it is scored as the sleep stage associated with those waves.
-
If an epoch lacks characteristic waves, scoring considers the preceding epochs’ stages and characteristic waves.
-
If an epoch contains multiple characteristic waves associated with different sleep stages, it is scored as the dominant sleep stage.
In this study, we employed In-home EEG, an EEG measurement device developed by S’UIMIN20. This device is equipped with four electrodes positioned at Fp1, Fp2, M1, and M2, and it independently records their electrical potentials. Additionally, In-home EEG also records the contact resistance of each electrode, allowing us to easily identify problematic electrodes. For further details, please refer to the “In-home EEG” section.
Proposed method
As mentioned in the Introduction, our proposed method is a variation of ensemble methods, with distinct characteristics in its small models and voting process compared to typical ensemble methods. Specifically, the small models use different input signals and electrodes (Table 1), and models deemed problematic are excluded from the voting process.
The voting is conducted by comparing the averaged “certainty values,” calculated by the small models. Concretely, the voting output Y for the input X is calculated as follows:
where N is the number of small models, \(C^s_i\) is the certainty-value function for stage s for the i-th small model, and \(X_i\) is the signal set assigned to the i-th small model. These small models use different input signals, so the variance of scoring accuracy tends to be significant. Therefore, we employed the above voting method to give more weight to the scoring results of the small models with high certainty values.
Fortunately, In-home EEG directly measures the contact resistance of each electrode. We used these values to identify problematic electrodes. Any electrode with a contact resistance exceeding \(100\, \textrm{k}{\Omega }\) was considered noisy or detached, and the corresponding small models were excluded from the voting process. For example, if the Fp1 electrode was detached, all models except the third one (Table 1) were excluded from voting. Notably, this voting process with exclusion was conducted on an epoch-by-epoch basis.
The electrodes M1 and M2 were placed at the mastoids and generally used as references because their electrical potential is relatively stable. However, we found that the M1-M2 signal contains some EMG actively occurring around the jaw and throat. Therefore, we employed this signal as an alternative to the submental EMG signal.
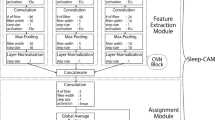
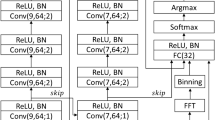
Fig 3 presents an example of the structure and hyperparameters of a small model, adapted from a deep learning model proposed in prior research19. This adaptation is specifically designed for home measurement devices, with a focus on adjusting the number of input channels. Note that the hyperparameters, such as number of filter, filter and batch size, are the same as those used in the prior research19.
This deep-learning-based model receives one-epoch-length biological signals and outputs a certainty value for the sleep stage. This small model achieved high scoring accuracy with minimal computational costs. The experiment showed that this model scored the sleep stages with 80.6% accuracy (Table 2) when it employed Fp1-\(\mathrm{M_{ave}}\), Fp2-\(\mathrm{M_{ave}}\), and Fp1-Fp2 signals. The training process was conducted using cross-entropy loss and the Adam optimizer (lr = \(5*10^{-6}\), batch size = 32) until the training iteration reached 50 times. We did not employ any early-stopping methods.
Structure and Hyperparameters of small models: each small model uses the same structure and hyperparameters, except for the number of input signals. The models consist of two main modules: a Feature Extraction Module and an Assignment Module. These correspond to the detection of characteristic waves in manual scoring and the allocation of sleep stages, respectively. The structure and hyperparameters of these models have been optimized based on existing research19 to achieve high scoring accuracy with minimal computational requirements.
Results
Evaluation experiment
To verify the efficacy of our proposed method, we conducted five-fold cross-validation using 297 whole-night sleep records obtained by the In-home EEG from 53 participants at their homes. The training and test samples comprised sleep records obtained from different participants. For more details, please refer to the “Datasets” section.
Table 2 illustrates the change in scoring accuracy resulting from the apprication of the proposed method. The reference is a single model equivalent to the first model in Table 1, which achieved reasonably high accuracy in the absence of contact problems. According to experimental results, the proposed method enhanced scoring accuracy by 8.3 points (81.0–72.7%) for epochs affected by contact problems. Furthermore, the method minimized the decline in scoring accuracy caused by contact problems from 7.9 points (80.6–72.7%) to 0.3 points (81.3–81.0%), demonstrating its effectiveness in preserving scoring accuracy levels.
Fig 4 illustrates the hypnogram when the proposed method is applied to a sleep record with contact failures. In this figure, gray shaded regions represents periods where the M2 electrode experienced contact failure. In response, human experts mitigated the impact of this failure by excluding the M2 electrode, to ensure accurate scoring (Fig 4a).
The reference model was unable to ignore the M2 electrode. Typically, noise from contact failures contains a high-frequency component, which can be mistaken for body movement and lead to a biased scoring towards W (Fig 4b). In contrast, our proposed method excluded the models using the M2 electrode from the voting process and achieved scoring process similar to that of human experts, who disregarded M2 (Fig 4c).
Changes in hypnogram with and without employing the proposed method. The gray shaded areas indicate periods with contact failure in the M2 electrode. (a) Scoring results by a human expert, with a re-montage performed in response to the contact failure of M2. (b) Scoring results without using the proposed method (reference model). Signals using M2 contain high-frequency noise, potentially due to body movement, leading to a biased determination toward Stage W. (c) Scoring results with the proposed method. The proposed method uses only a model that does not use the M2 electrode in the event of contact failure, resulting in a scoring that is not biased towards W and similar to human expert results.
Additionally, the proposed method also enhanced accuracy for epochs without contact problems to 81.3% (Table 2). Considering that the inter-rater reliability among human experts using PSG equipment is 82.0%21, we can conclude that our proposed model achieved nearly the same level of accuracy as experts.
To further evaluate the efficacy of our proposed method on signals without contact failures, we utilized the Sleep Heart Health Study (SHHS) dataset22. This dataset comprises 5793 sleep records obtained from an equal number of subjects. For this study, we conducted the five-fold cross-validation on 5353 subjects’ sleep records, after excluding 440 records due to very high amplitude or improper zero-point adjustment.
This dataset only contains two types of signals: C3-M2 and C4-M1. Therefore, our proposed method was implemented by using an ensemble of three small models: one using only the C3-M2 signal, another using only the C4-M1 signal, and a third using both signals. To accommodate differences in sampling frequency, we adjusted the filter width of the convolutional layer in the small models to match the same time duration as in the original dataset. Note that all trainable parameters were retrained from scratch, and early stopping was employed in this experiment. Specifically, the training process was repeated until the validation accuracy remained unchanged for five consecutive training epochs, or until the number of iterations reached 80.
Before delving into analysis, we would like to address the issues encountered with the small models in this experiment. Both the proposed method and the Typical Ensemble method exhibited decreased accuracy and F1 scores on the SHHS dataset (Table 3). The SHHS dataset has a less balanced distribution of sleep stages compared to the In-home EEG data, which may have contributed to the decreased performance of the small models. This may slightly diverge from the main theme of this paper, but implementing sample balancing techniques could potentially yield improved results.
Regarding the experimental results, the proposed method demonstrated a tendency to improve classification accuracy on the SHHS dataset (Table 3). However, this improvement was less pronounced compared to the In-home EEG dataset. This could be attributed to the smaller number of small models used and the presence of models that rely on only one signal, which are factors likely to affect the overall classification accuracy. Additionally, the SHHS dataset’s bias towards older subjects may have also impacted accuracy compared to the more diverse In-home EEG dataset.
In this dataset, the Typical Ensemble method exhibited better scoring accuracy than our proposed method. The difference in accuracy can be attributed to the performance variation among the small models. Specifically, the models in our proposed method that utilized one-signal-input achieved an accuracy of approximately 78%, which is significantly lower than the over 80% accuracy achieved by the small models in the Typical Ensemble.
One reason for this discrepancy in accuracy could be attributed to the limited number of input signals. As shown in Table 1, small models #3 and #4, which have fewer input signals, exhibited nearly 1 to 2 points lower accuracy compared to the other models. Additionally, there is a possibility that the signals contain unidentified noise. In such a case, the scoring accuracy of the one-signal-input models would decrease significantly.
To maximize the utility of our proposed method, it appears necessary to:
-
1.
Increase the variety of signals that can be used as inputs, enabling each small model to process multiple signals.
-
2.
Ensure reliable detection of noise in the signals.
These steps should help enhance the overall accuracy of the proposed method.
The AASM guidelines recommend measuring EEG with six channels and selecting reference signals based on electrode contact quality and noise. Recently, even simplified sleep monitors have improved to measure multiple channels and perform re-montage using the potential difference with Fpz20,26. Our method would be effective with these types of devices.
Although the proposed method has improved scoring accuracy, its computational costs were approximately six-times higher than those of the reference model (Table 2 (c)). This is primarily because we used six small models equivalent to the reference model. While incorporating more small models is expected to enhance scoring accuracy and enable better handling of electrodes with contact failures, it unfortunately comes at the expense of increased computational costs.
Comparison with a typical ensemble method and anti-noise methods
We compared the performance of our method with a typical ensemble method and two anti-noise methods to assess their effectiveness in mitigating the effect of problematic signals and improving scoring accuracy. As previously mentioned, the ensemble method can enhance overall scoring accuracy but lacks mechanisms to reduce the impact of contaminated signals. In contrast, anti-noise methods cannot improve scoring accuracy for clear records.
The compared ensemble method consisted of six small models with the identical input signals as the reference model. Each model shared the same structures but was optimized using different sets of training samples. Specifically, the small models selected samples with overlaps until the number of selected samples matched that of the proposed method. This limitation could lead to poor scoring accuracy of each small model. However, we deemed it a fair comparison because the total number of training samples for the entire scoring system remained consistent.
In this comparison, we focused on two anti-noise methods that offer relatively simple solutions for dealing with problematic signals. To our knowledge, these methods do not have established names, and this paper refers to them as the re-montage and signal copying methods.
Montage is the method used to derive biological signals by subtracting the electrical potentials of two electrodes. Typically, one measuring electrode from Fp1 and Fp2 and one reference electrode from M1 and M2 are selected. In the re-montage method, the contact state of each electrode is assessed using some method, and the best measuring/reference electrodes are used. For example, if there is a contact problem with electrodes Fp1 and M1, Fp2-M2 signal will be used in the scoring process instead. Contact state assessment often involves metrics such as signal kurtosis, but in this study, we directly measure the contact resistance of the electrodes.
Although this method is one of the most popular in the automated sleep stage scoring systems16, it has limitations regarding the number of input signals and electrode combinations. For example, with the M1-M2 combination, there are no alternative electrodes available if either electrode encounters a problem. Therefore, the scoring model may have limited information to score sleep stages.
The signal copying method is similar to the re-montage method, but can use two EEG signals. Specifically, we consider them as Fp1-\(\mathrm{M_{ave}}\) and Fp2-\(\mathrm{M_{ave}}\). \(\mathrm{M_{ave}}\) is the averaged potential of M1 and M2. This method overwrites the problematic signal with another clean counterpart: if the Fp1 electrode has a contact problem, the Fp1-\(\mathrm{M_{ave}}\) signal is replaced by the Fp2-\(\mathrm{M_{ave}}\) signal. Therefore, the scoring model temporarily receives two identical signals. If the M1 electrode becomes detached, Fp1-M2 and Fp2-M2 are used. Although this operation for reference electrodes does not follow the principle of “signal copying,” it aligns more closely with manual scoring practices. This method also cannot employ the M1-M2 signal, but the scoring accuracy is expected to be higher than that of the re-montage method.
We applied these two anti-noise methods to the deep learning models, whose structures follow that of Fig 3, but with adjustments made to the first convolutional layer to accommodate varying numbers of input signals.
Table 2 shows the comparison results. As anticipated, the typical ensemble model improved the scoring accuracy, but the improvements were not remarkable. A significant degradation in scoring accuracy remained.
Contrary to expectations, the re-montage method did not yield any improvement. The scoring accuracy for epochs without contact problems decreased. This outcome suggests that restricting the number of input signals could have a significant impact on scoring accuracy. Similar to the re-montage method, the signal-copying method could not improve the scoring accuracy for clear signals. However, it proved to be a feasible solution for contact problems. The accuracy improved by 6.7 points with minimal additional computational costs.
Discussion
The experimental results demonstrated that the proposed method effectively mitigated the deterioration in scoring accuracy caused by contact problems, reducing it from 7.9 to 0.3 points. Moreover, it achieved high scoring accuracy for records affected by contact issues, surpassing the performance of the reference method for clear records. Additionally, it improved the scoring accuracy by 0.7 points for clear sleep records. The proposed model was the only method capable of simultaneously enhancing the overall scoring accuracy and minimize the impact of unreliable signals.
However, two practical challenges persist. The primary issue is that electrode contact is not the sole cause for the deterioration of scoring accuracy. Our study confirmed that the proposed method could not enhance scoring accuracy for certain records, where it ranged only from 55 - 65%. These records exhibited a higher prevalence of N1 epochs compared to others, possibly influenced by factors such as aging, sleep apnea syndrome (SAS), and so on23,24. Such variations in sleep-stage distribution can diminish scoring accuracy by altering the probabilities used in Bayesian estimation. Addressing this issue will be a focus of our future research efforts.
The computational cost associated with the proposed method presents another challenge. In our approach, the small models share the same structure and hyperparameters, including the number of filters in each layer, despite utilizing different numbers of input signals. Consequently, the number of input signals contributes minimally to the computational demand required for training and scoring of these small models. Assuming a constant computational cost of each small model, the overall computational complexity of our method is nearly linear in relation to the number of small models used.
In evaluating the practicality of our method, we encounter a significant a notable dilemma regarding computational efficiency and scoring accuracy. On one hand, the desire to minimize the overall computational time drives us towards employing simple small models, which inherently have lower computational demands. However, the overall accuracy of our method is heavily dependent on the performance of these individual small models. Typically, models with higher accuracy tend to have more complex structures, which in turn require greater computational resources. Thus, we are faced with a delicate balance: achieving high accuracy through more complex models while striving to keep a manageable computational load.
Parallel execution of small models presents a potential solution to this problem. The computations (training and scoring) of these small models are completely independent of each other, allowing for easy parallelization. However, such parallel execution often requires the use of GPU-based high-performance computing, which may not be a feasible solution for general sleep clinics due to the specialized hardware requirements.
In this paper, we evaluate the performance of the proposed method in scenarios involving single electrode channels with poor contact. Now, we turn our attention to cases involving multiple electrodes experiencing issues. In conclusion, while the principles of our method could be applied to such cases, we find it impractical for home measurement devices. Not only automated, but also manual sleep stage scoring requires signals between measurement and reference electrodes to achieve high scoring accuracy. While we can obtain such signals in cases with a single problematic channel, it is rare to obtain these signals when there are multiple problematic channels. For instance, our dataset contained only 12 such epochs out of 289 epochs where multiple electrodes had issues. This is in stark contrast to the epochs with a single problematic channel, which total 7484 epochs (3.4%) (Table 4). Given their rarity, addressing multiple problematic electrodes may not be practical. This pattern is likely attributable to the close proximity of electrode placements and similar measurement conditions. We have not confirmed this trend in other datasets, but we believe it may be observed in others as well. In contrast, considering the possibility of poor contact affecting multiple channels would be highly beneficial for PSG devices that typically measure EEG with six channels.
Methods
All procedures were conducted in accordance with the Ethical Guidelines for Medical and Health Research Involving Human Subjects at the University of Tsukuba and the Declaration of Helsinki. The study received approval from the Tsukuba Clinical Research and Development Organization (T-CReDO) of the University of Tsukuba (Approved ID# H29-177) and the Ethics Committee of the Center for Computational Sciences at the University of Tsukuba (Approved ID# 19-001). The study protocol (UMIN000029911) was registered with the University Hospital Medical Information Network Center. All subjects were over 19 years old, and informed consent was obtained from each participant.
Datasets
In this study, we primarily used our original dataset to evaluate the performance of the proposed ensemble method. This dataset consists of 297 whole-night sleep records obtained using In-home EEG from 53 adult participants. The dataset’s properties are shown in Table 4. All measurements were conducted at the participants’ homes, with the participants themselves placing the electrodes. Please note that there are 289 epochs with multiple problematic electrodes out of 220372 (0.1%). These epochs were excluded during the training/testing process.
A sleep expert who achieved the intra-rater reliability of \(92.1\%\) with PSG equipment scored all sleep records. She scored the In-home EEG records according to AASM rules, achieving an agreement rate of \(86.8\%\), with the scoring results for simultaneously measured PSG records.
To further confirm the effectiveness of our proposed method on signals without contact failures using a more extensive dataset, we employed the Sleep Heart Health Study (SHHS) dataset22. This dataset does not contain information on the contact resistance of each electrode. Therefore, all measurement records and epochs were treated as if they had no contact failures. Although the dataset includes a large number of subjects, it is biased towards older individuals, resulting in slightly lower scoring accuracy compared to the In-home EEG data.
In-home EEG
We measured the sleep records with “In-home EEG version 2.1,” by S’UIMIN Inc. (Tokyo, Japan)20. This device uses four electrodes; two for the forehead (Fp1, Fp2) and two for the mastoid (M1, M2). As aforementioned, the M1 and M2 electrodes were mainly used as references, but also simulated a submental EMG signal. The electrical potentials of all electrodes were measured at the sampling frequency of 200 Hz and filtered with a high-pass filter with a cutoff frequency of 0.05 Hz.
Furthermore, this device also measured the contact resistance of these electrodes every 30 s (one epoch). These resistance values were used to identify the contact failures. Specifically, an electrode with a resistance value exceeding \(100\, \textrm{k}{\Omega }\) was regarded as problematic in the experiment.
Performance indices
To evaluate the performance of the proposed methods, we calculated the scoring accuracy, kappa statistics, and F1 score for the epochs with and without contact problems. The formulas used for these metrics are as follows:
where \(E_{(s,u)}\) represents the number of epochs scored as Stages s and u by the human expert and the scoring system, respectively, and M is the total number of epochs used for testing. As mentioned above, we assumed that the human expert always provides the correct sleep-stage label. Thus, the accuracy was defined as being equal to the inter-rater reliability between the expert and system.
The kappa statistic was used to evaluate the scoring agreement between the expert and system. Unlike simple accuracy calculations, kappa statistics consider variations in the distribution of each sleep stage30. Typically, a kappa statistic exceeding 0.8 indicates perfect agreement between the two results30,31. The F1 Score is another evaluation metric suited for imbalanced data, as it calculates the harmonic mean of precision and recall. It is commonly used in information science and engineering.
Note that these statistics were calculated separately for epochs with and without contact problems.
Computer hardware
All experiments using the In-home EEG dataset, and some experiments using the SHHS dataset, were conducted using the following workstation:
- CPU:
-
Intel(R) Xeon(R) Gold 6154 CPU @ 3.00 GHz
- GPU:
-
Tesla V100 SXM2 32GB \(\times\) 8 Please note that only one of these GPUs was used in the experiments.
- Memory:
-
754 GB
- OS:
-
Ubuntu 16.04.7 LTS
- Python:
-
Version 3.6.9
- Tensorflow:
-
TensorFlow-GPU 2.3.0 & 2.0.333
Experiments using the SHHS dataset also utilized the following two workstations.
1.
- CPU:
-
AMD EPYX 7643 48-Core Processor @ 1.50 GHz
- GPU:
-
RTX A6000 50 GB \(\times\) 6
- Memory:
-
1.0 TB
- OS:
-
Ubuntu 20.04.4 LTS
- Python:
-
Version 3.6.9
- Tensorflow:
-
TensorFlow 2.10.033
2.
- CPU:
-
Intel(R) Xeon(R) Platinum 8180 @ 2.50 GHz
- GPU:
-
Tesla V100 SXM2 32GB \(\times\) 4
- Memory:
-
1.5 TB
- OS:
-
Ubuntu 18.04.3 LTS
- Python:
-
Version 3.6.9
- Tensorflow:
-
TensorFlow-GPU 2.0.333
To implement the proposed method and conduct the experiments, we used Keras34 integrated with TensorFlow version. We also used Cygnus32 in some preliminary experiments, a high-performance computer managed by the Center for Computational Sciences at the University of Tsukuba.
Conclusion
In this study, we proposed an ensemble-based aimed at mitigating the impact of contact problems and enhancing overall accuracy. Unlike typical ensemble methods, our approach utilizes small models with distinct sets of input signals rather than varied training samples. Additionally, it minimizes the influence of contact problems by excluding models with problematic input signals from the voting process. Experimental results demonstrate that this approach effectively reduces the decline in scoring accuracy and enhances scoring accuracy also for clear sleep records. These findings suggest that the proposed model address multiple challenges associated with In-home sleep measurement.
Several important future research issues remain regarding scoring accuracy using In-home EEG devices. These include individual differences. As previously stated, the SAS patients have different sleep tendencies, and such a difference could decrease the automated scoring accuracy. To achieve more stable automated sleep stage scoring, these issues will be a focus of our future research efforts.
Data availibility
The datasets analyzed during the current study are the property of S’UIMIN inc. If you wish to use this dataset for your own research works, please contact the corresponding authors and S’UIMIN inc.
Change history
21 January 2025
A Correction to this paper has been published: https://doi.org/10.1038/s41598-025-85854-x
References
Knutson, K. L. & Cauter, E. V. Associations between sleep loss and increased risk of obesity and diabetes. Ann. NY. Acad. Sci.[SPACE]https://doi.org/10.1196/annals.1417.033 (2008).
Nutt, D., Wilson, S. & Paterson, L. Sleep disorders as core symptoms of depression. Dialogues in Clinical Neuroscience, 10, 329–336; https://doi.org/10.31887/DCNS.2008.10.3/dnutt (2008).
Redline, S. et al. Obstructive sleep apnea-hypopnea and incident stroke: the sleep heart health study. Am. J. Respir. Crit. Care Med. 182(2), 269–277. https://doi.org/10.1164/rccm.200911-1746OC (2010).
Gottlieb, D. J. et al. Prospective study of obstructive sleep apnea and incident coronary heart disease and heart failure. Circulation 122(4), 352–360. https://doi.org/10.1161/CIRCULATIONAHA.109.901801 (2010).
Hafner, M., Stepanek, M., Taylor, J., Troxel, W. M. & Stolk, C. V. Why sleep matters - the economic costs of insufficient sleep: A cross-country comparative analysis. RAND Corporation (2016), https://www.rand.org/pubs/research_reports/RR1791.html available at August 15th, 2023.
Malhotra, A. et al. Performance of an automated polysomnography scoring system versus computer-assisted manual scoring. Sleep 36, 573–582 (2013).
Boe, A. J. et al. Automating sleep stage classification using wireless, wearable sensors. npj Digital Med. 2, 9. https://doi.org/10.1038/s41746-019-0210-1 (2019).
Sridhar, N. et al. Deep learning for automated sleep staging using instantaneous heart rate. npj Digital Med. 3, 10. https://doi.org/10.1038/s41746-020-0291-x (2020).
Myllymaa, S. et al. Assessment of the suitability of using a forehead EEG electrode set and chin EMG electrodes for sleep staging in polysomnography. J. Sleep Res. 25, 636–645. https://doi.org/10.1111/jsr.12425 (2016).
Levendowski, D. J. et al. The accuracy, night-to-night variability, and stability of frontpolar sleep electroencephalography biomarkers. J. Clin. Sleep Med. 13, 791–803. https://doi.org/10.5664/jcsm.6618 (2017).
Mikkelsen, K. B. et al. Accurate whole-night sleep monitoring with dry-contact ear-EEG. Sci. Rep. 9, 12. https://doi.org/10.1038/s41598-019-53115-3 (2019).
Arnal, P. J. et al. The Dreem Headband compared to polysomnography for electroencephalographic signal acquisition and sleep staging. Sleep 43(11), 13. https://doi.org/10.1093/sleep/zsaa097 (2020).
Tabar, Y. R. et al. Ear-EEG for sleep assessment: a comparison with actigraphy and PSG. Sleep Breath. 25, 1693–1705. https://doi.org/10.1007/s11325-020-02248-1 (2021).
Fiorillo, L. et al. Automated sleep scoring: A review of the latest approaches. Sleep Med. Rev.[SPACE]https://doi.org/10.1016/j.smrv.2019.07.007 (2019).
Faust, O., Razaghi, H., Barika, R., Ciaccio, E. J. & Acharya, U. R. A review of automated sleep stage scoring based on physiological signals for the new millennia. Comput. Methods Programs Biomed. 176, 81–91. https://doi.org/10.1016/j.cmpb.2019.04.032 (2019).
Stephansen, J. B. et al. Neural network analysis of sleep stages enables efficient diagnosis of narcolepsy. Nat. Commun. 9, 15. https://doi.org/10.1038/s41467-018-07229-3 (2018).
Zhang, L., Fabbri, D., Upender, R. & Kent, D. Automated sleep stage scoring of the Sleep Heart Health Study using deep neural networks. Sleep 42(11), 10. https://doi.org/10.1093/sleep/zsz159 (2019).
Sokolovsky, M., Guerrero, F., Paisarnsrisomuk, S., Ruiz, C. & Alvarez, S. A. Deep learning for automated feature discovery and classification of sleep stages. IEEE/ACM Trans. Comput. Biol. Bioinf. 17, 1835–1845. https://doi.org/10.1109/TCBB.2019.2912955 (2020).
Horie, K. et al. Automated sleep stage scoring employing a reasoning mechanism and evaluation of its explainability. Sci. Rep. 12, 19. https://doi.org/10.1038/s41598-022-16334-9 (2022).
S’UIMIN inc. S’UIMIN inc. https://www.suimin.co.jp/ available at August 15th, (2023).
Danker-Hopfe, H. et al. Interrater reliability between scorers from eight European sleep laboratories in subjects with different sleep disorders. J. Sleep Res. 13(1), 63–69. https://doi.org/10.1046/j.1365-2869.2003.00375.x (2004).
Quan, S. F. et al. The Sleep Heart Health Study: design, rationale, and methods. Sleep 20(12), 1077–1085 (1997).
Schlemmer, A., Parlitz, U., Luther, S., Wessel, N. & Penzel, T. Changes of sleep-stage transitions due to ageing and sleep disorder. Philosophical Trans. Royal Soc. A 373, 16. https://doi.org/10.1098/rsta.2014.0093 (2015).
Korkalainen, H. et al. Accurate deep learning-based sleep staging in a clinical population with suspected obstructive sleep apnea. IEEE J. Biomed. Health Inf. 24(7), 2073–2081. https://doi.org/10.1109/JBHI.2019.2951346 (2020).
Beacon Biosignals, Inc. Dreem Labs for Clinical Trial. https://dreem.com/clinicaltrials available at August 15th, (2023).
Advanced Brain Monitoring. Sleep Profiler. https://www.advancedbrainmonitoring.com/products/sleep-profiler available at June 14th, (2024).
Breiman, L. Bagging predictors. Machine learn. 24, 123–140. https://doi.org/10.1007/BF00058655 (1996).
Freund, Y & Schapire, R. Experiments with a new boosting algorithm. In Proceedings of the Thirteenth International Conference on Machine Learning, 148–156 (1996).
Berry, R.et al. The AASM Manual for the scoring of sleep and associated events: rules, terminology and technical specifications. Version 2.5. American Academy for Sleep Medicine (2018).
Landis, J. R. & Koch, G. G. The measurement of observer agreement for categorical data. Biometrics 33(1), 159–174 (1977).
Krippendorff, K. Content analysis: An introduction to its methodology (Sage Publications, 1980).
Center for Computational Sciences, University of Tsukuba. Overview of Cygnus: a new supercomputer at CCS. https://www.ccs.tsukuba.ac.jp/wp-content/uploads/sites/14/2018/12/About-Cygnus.pdf available at August 15th, (2023).
Abadi, M. et al. TensorFlow:Large-scale machine learning on heterogeneous systems. https://static.googleusercontent.com/media/research.google.com/en//pubs/archive/45166.pdf (2015). Software available from tensorflow.org.
Chollet, F. et al. Keras (2015). Software available from keras.io
Acknowledgements
This work was partially supported by AMED (Grant Number JP21zf0127005), the MEXT Program for Building Regional Innovation Ecosystems, MEXT Grant-in-Aid for Scientific Research in Innovative Areas (Grant Number 15H05942Y), the WPI program from Japan’s MEXT, JSPS KAKENHI (Grant Numbers 17H06095 and JP22K19802), the FIRST program from JSPS, JST-Mirai Program (Grant Number JPMJMI19D8), and the joint research project “Social Application of Mobility Innovation and Future Social Engineering Research Phase IV,” a collaboration between Toyota Motor Corporation and the University of Tsukuba. Additionally, this study involved collaborative research with S’UIMIN inc., where M. Yanagisawa serves as a board member, and they also provided the sleep cohorts for this research. The computational resources from Cygnus32, as provided by the Multidisciplinary Cooperative Research Program in the Center for Computational Sciences at the University of Tsukuba, were also utilized in this study.
Author information
Authors and Affiliations
Contributions
K. Horie conceived the main idea of the proposed method; K. Horie, and H. Kitagawa designed the experiments; R. Miyamoto implemented the methods and conducted experiments using the in-home EEG dataset; L.Ota conducted experiments using the SHHS dataset; K. Horie, R. Miyamoto, L. Ota, and H. Kitagawa analyzed the experimental results; F. Kawana, Y. Suzuki, T. Abe, T. Kokubo, and M. Yanagisawa provided the dataset and background knowledge in clinical sleep medicine; and K. Horie, R. Miyamoto, and H.Kitagawa drafted the paper.
Corresponding authors
Ethics declarations
Competing interests
We have read the journal’s policy and the authors of this manuscript declare the following competing interests: Y. M. has previously received research grant support from MEXT, JSPS, AMED, JST and TOYOTA. He is a board member of S’UIMIN inc., receives a salary from the company, and also owns shares in it. T. K. has previously received research grant support from AMED, JSPS, JST, and TOYOTA. He is a board member of S’UIMIN inc., receives a salary from the company, and also owns shares in it. H. K. has previously received research grant support from MEXT, JSPS, AMED, JST, TOYOTA and S’UIMIN inc. He owns shares in the S’UIMIN inc. F. K. has been subcontracted by S’UIMIN inc. The other authors have declared that no competing interests exist. While S’UIMIN inc. provided the sleep cohorts for this study, they had no influence on the study design, data analysis, decision to publish, or manuscript preparation. However, it should be noted that publishing this research could benefit S’UIMIN inc.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The original online version of this Article was revised: In the original version of this Article Kazumasa Horie, Ryusuke Miyamoto, Leo Ota, Takashi Abe, Yoko Suzuki, Fusae Kawana & Hiroyuki Kitagawa were incorrectly affiliated with ‘S’UIMIN inc., Shibuya, Japan’. The affiliation and the correct affiliated authors are mentioned here: S’UIMIN inc., Shibuya, Japan. Toshio Kokubo & Masashi Yanagisawa.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Horie, K., Miyamoto, R., Ota, L. et al. An ensemble method for improving robustness against the electrode contact problems in automated sleep stage scoring. Sci Rep 14, 21894 (2024). https://doi.org/10.1038/s41598-024-72612-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-024-72612-8